SetElementBoneQuaternion: Difference between revisions

From Multi Theft Auto: Wiki
Jump to navigation Jump to search
m (Stylistic corrections)
(Remove obsolete Requirements section)
 
(6 intermediate revisions by one other user not shown)
Line 2: Line 2:
{{Client function}}
{{Client function}}


{{New feature/item|3.0161|1.6.0|22722|
{{New feature/item|3.0161|1.6.0|22741|
This function determines how a particular bone rotates in relation to the element.<br/>
This function determines how a particular bone rotates in relation to the element.<br/>
The use of [https://en.wikipedia.org/wiki/Quaternion quaternions] are more effective and do not generate issues like gimbal lock that might arise with [https://en.wikipedia.org/wiki/Euler_angles Euler angles], so they are a preferable choice for rotation.
The use of [https://en.wikipedia.org/wiki/Quaternion quaternions] are more effective and do not generate issues like gimbal lock that might arise with [https://en.wikipedia.org/wiki/Euler_angles Euler angles], so they are a preferable choice for rotation.
Line 9: Line 9:
{{Tip|If you want to attach an element to a bone, see [[attachElementToBone]].}}
{{Tip|If you want to attach an element to a bone, see [[attachElementToBone]].}}
{{Note|If you want to apply the rotation, [[updateElementRpHAnim]] must be called after this function.}}
{{Note|If you want to apply the rotation, [[updateElementRpHAnim]] must be called after this function.}}
==Syntax==  
==Syntax==  
<syntaxhighlight lang="lua">
<syntaxhighlight lang="lua">
bool setElementBoneQuaternion(element ped, int bone, float x, float y, float z, float w)
bool setElementBoneQuaternion(element ped, int bone, float x, float y, float z, float w)
</syntaxhighlight>  
</syntaxhighlight>  
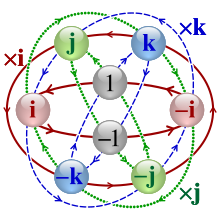
[[File:Cayley_Q8_multiplication_graph.png|thumb|[https://en.wikipedia.org/wiki/Cayley_graph Cayley Q8 graph] showing the six cycles of multiplication by <span style="color: red;">'''i'''</span>, <span style="color: green;">'''j'''</span> and <span style="color: blue;">'''k'''</span>.]]


===Required Arguments===
===Required Arguments===
Line 33: Line 36:


==Example==  
==Example==  
This example rotates the player's head 180 degrees around an arbitrary axis.<br/>
This example rotates the player's pelvis 180 degrees around an arbitrary axis.<br/>
The use of [[updateElementRpHAnim]] is necessary here as it applies the rotation.
The use of [[updateElementRpHAnim]] is necessary here as it applies the rotation.
<syntaxhighlight lang="lua">
<syntaxhighlight lang="lua">
Line 47: Line 50:
)
)
</syntaxhighlight>
</syntaxhighlight>
==Requirements==
{{Requirements|n/a|1.6.0-9.22722}}


==See Also==
==See Also==
{{Client_element_functions}}
{{Client_element_functions}}

Latest revision as of 17:35, 7 November 2024

ADDED/UPDATED IN VERSION 1.6.0 r22741:

This function determines how a particular bone rotates in relation to the element.
The use of quaternions are more effective and do not generate issues like gimbal lock that might arise with Euler angles, so they are a preferable choice for rotation.


[[{{{image}}}|link=|]] Tip: If you want to attach an element to a bone, see attachElementToBone.
[[{{{image}}}|link=|]] Note: If you want to apply the rotation, updateElementRpHAnim must be called after this function.

Syntax

bool setElementBoneQuaternion(element ped, int bone, float x, float y, float z, float w)
Cayley Q8 graph showing the six cycles of multiplication by i, j and k.

Required Arguments

  • ped: The element (ped or player) on which the bone's rotation will be set.
  • bone: The ID of the bone to set the quaternion of.
  • The bone ID corresponds to specific body parts like arms, legs, spine, head, etc.
  • The full list of bones is available in the Bone IDs reference.
  • x: The quaternion's coefficient of the 𝑖 component.
  • This represents the rotation around the x-axis and is the first imaginary part of the quaternion.
  • y: The quaternion's coefficient of the 𝑗 component.
  • This represents the rotation around the y-axis and is the second imaginary part of the quaternion.
  • z: The quaternion's coefficient of the 𝑘 component.
  • This represents the rotation around the z-axis and is the third imaginary part of the quaternion.
  • w: The real part of the quaternion.
  • This denotes the scalar component of the quaternion, which is linked to the angle of rotation.
  • The w value is derived by taking the cosine of half of the rotation angle, defined as the overall angle of rotation.

Returns

Returns true if the set was successful, otherwise returns an error message and returns false.

Example

This example rotates the player's pelvis 180 degrees around an arbitrary axis.
The use of updateElementRpHAnim is necessary here as it applies the rotation. 

local playerBone = 1
local playerBoneX, playerBoneY, playerBoneZ = 0.577, 0.577, 0.577
local playerBoneW = 0

addEventHandler("onClientPedsProcessed", root,
    function()
        setElementBoneQuaternion(localPlayer, playerBone, playerBoneX, playerBoneY, playerBoneZ, playerBoneW)
        updateElementRpHAnim(localPlayer)
    end
)

See Also



Retrieved from "https://wiki.multitheftauto.com/wiki/SetElementBoneQuaternion?oldid=81369"